什么是敏感度
- 上一篇我们谈到了系统的稳定裕度, 其中提到增益裕度和相位裕度两个指标. 现实情况中, 改变系统的参数会导致增益和相位同时变化, 从而使系统更快地趋向不稳定. 例如, 一个系统有20°相位裕度和10dB增益裕度, 但是实际改变闭环增益的时候, 可能在增加3dB, 相位滞后10°的时候, 系统已经不稳定了.
- 实际情况下单一的指标不好判断系统地稳定裕度, 有一个综合的指标来衡量系统对参数变化的承担能力, 这个指标就是敏感度.
- 我们用敏感度函数来计算系统的敏感度.
闭环系统敏感度函数
- 长这样:

Ms表示最大敏感度, S(jω)是敏感度函数, Ms就是取ω从0到无穷的S(jω)的最大值. - 接下来用Nyquist plot来推导敏感度函数:
- 有一个前置知识点是: 引入增益会导致一个系统的Nyquist plot在径向上放缩,因为从原点出发指向曲线上每一个点的向量幅度都受到这个增益的影响; 引入相位滞后会导致图像顺时针旋转. 并且造成一定的变形(向量幅值变化)
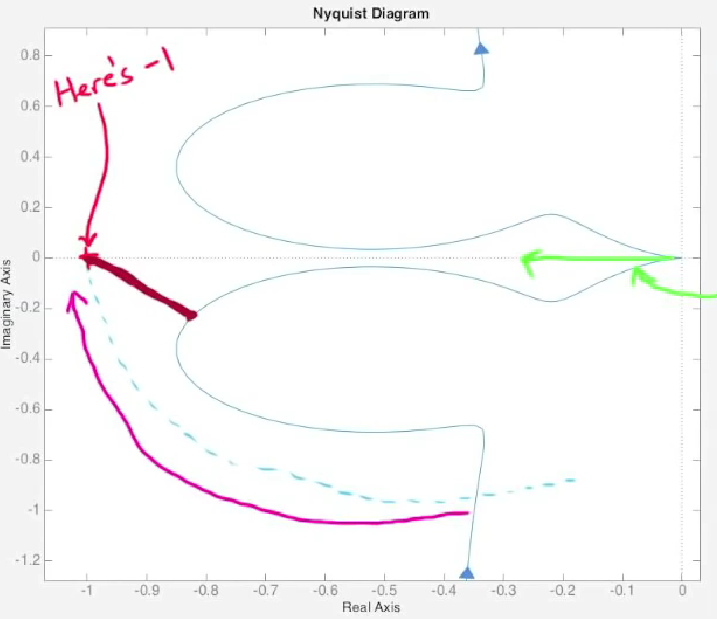
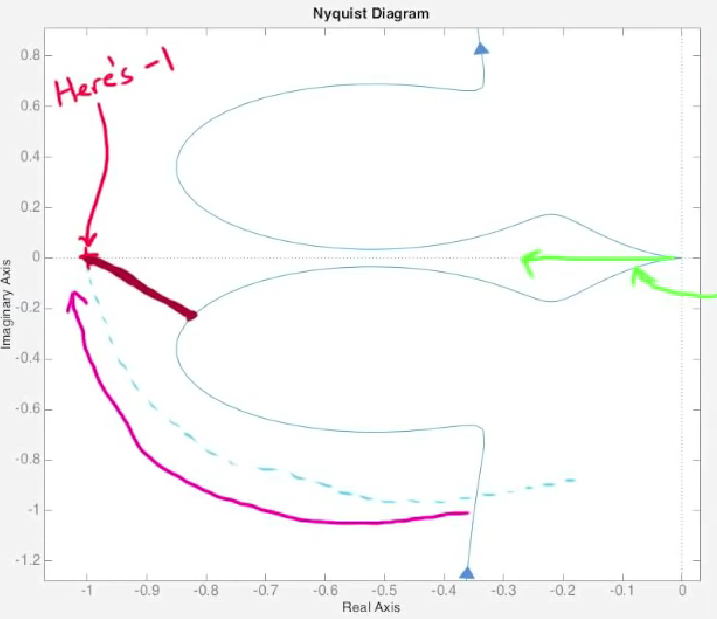
- 由这个知识点, 我们能够理解敏感度函数实际上考察的是Nyquist图上任意一点距离( -1, 0j )的最近距离是多少. 例如下图, 看似在实轴上Nyquist图距离( -1, 0j )很远, 但是由于图像有一个突出的瓣, 所以敏感度其实很高.
- 由于Nyquist plot的性质, 我们知道那些能看到的曲线基本上是由原s平面的jω轴映射过来的, 所以要表示任意一个Nyquist plot上的点, G(s)C(s)可以表示为G(jω)C(jω), 这个结果很可能是一个复数, 不妨设为 a+bj.
- 我们回看敏感度函数 S(jω) = 1 / ( 1 + G(jω)C(jω) ), 对它取绝对值则得到 |S(jω)| = 1 / |( 1 + G(jω)C(jω) )| = 1 / |( a - (-1) + bj - 0j )| = 1 / 任意一点到点( -1, 0j )的距离.
- 取倒数是因为更符合直觉, 距离越小取倒数就越大, 意味着敏感度越大.
- 综上, 敏感函数是可以推导出来的, 而不是天方夜谭的公式:

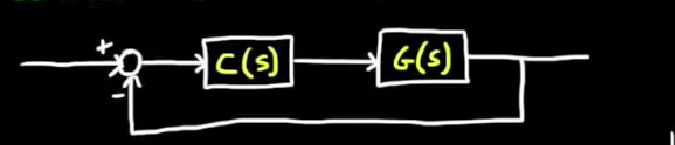
- 还可以画系统框图来直观地推导
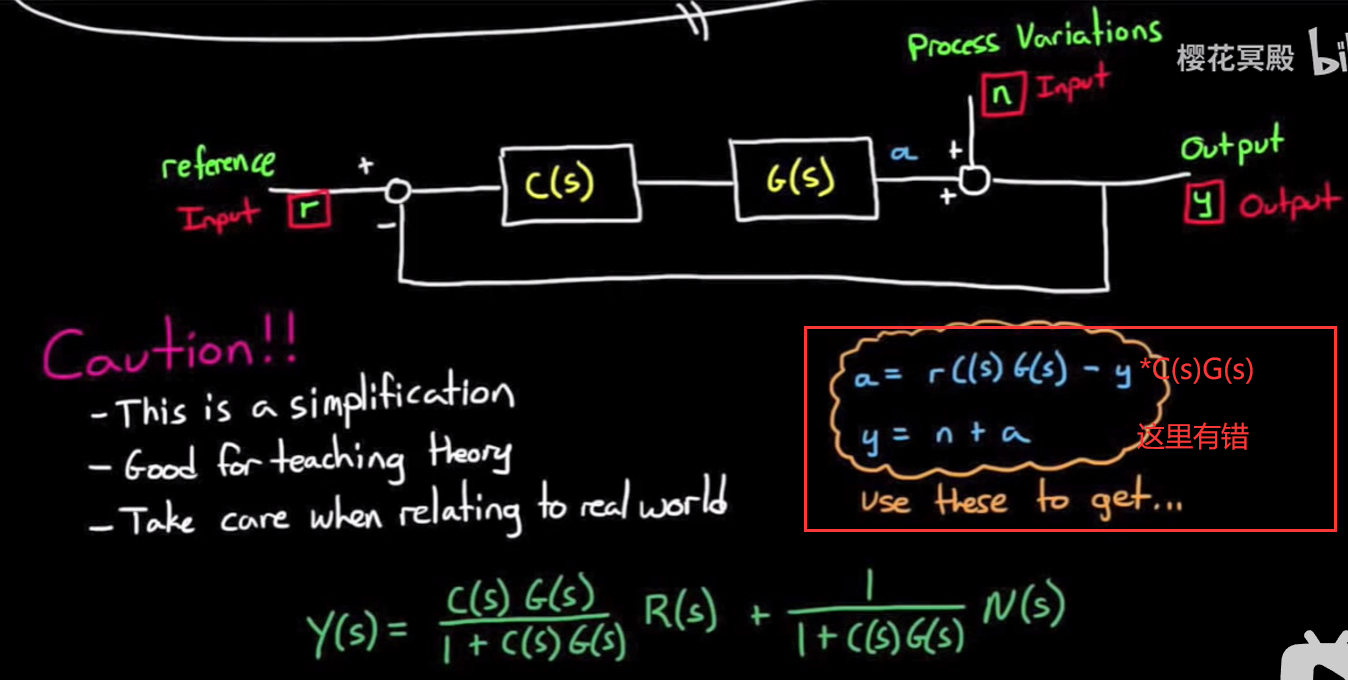
如上图,我们将所有系统可能受到的所有扰动抽象为n在最后加入则推导Y(s)的表达式在图片最底部, 可以看到除了正常的闭环系统传递函数对输入R(s)的作用, 还有一个部分是与扰动N(s)有关的, 而这个扰动能对Y(s)造成多大的影响, 由前面的系数决定, 可以发现这个系数正是敏感度函数.
如何降低敏感度
- 减少系统增益可以直接降低敏感度, 因为如前所述, 系统增益导致Nyquist plot径向放缩, 降低增益能直接让图像远离(-1, 0j), 但是有个坏处是系统增益减小导致系统响应变慢, 如下用matlab绘制的图像:
蓝色为原系统, 橙色为降低增益后的系统. 原系统的敏感度最大值来到3.5左右, 这一般是不可接受的, 正常值在1.3到2之间. 降低增益后虽然标称敏感度峰值降低到1.7左右, 但是系统响应明显变慢.
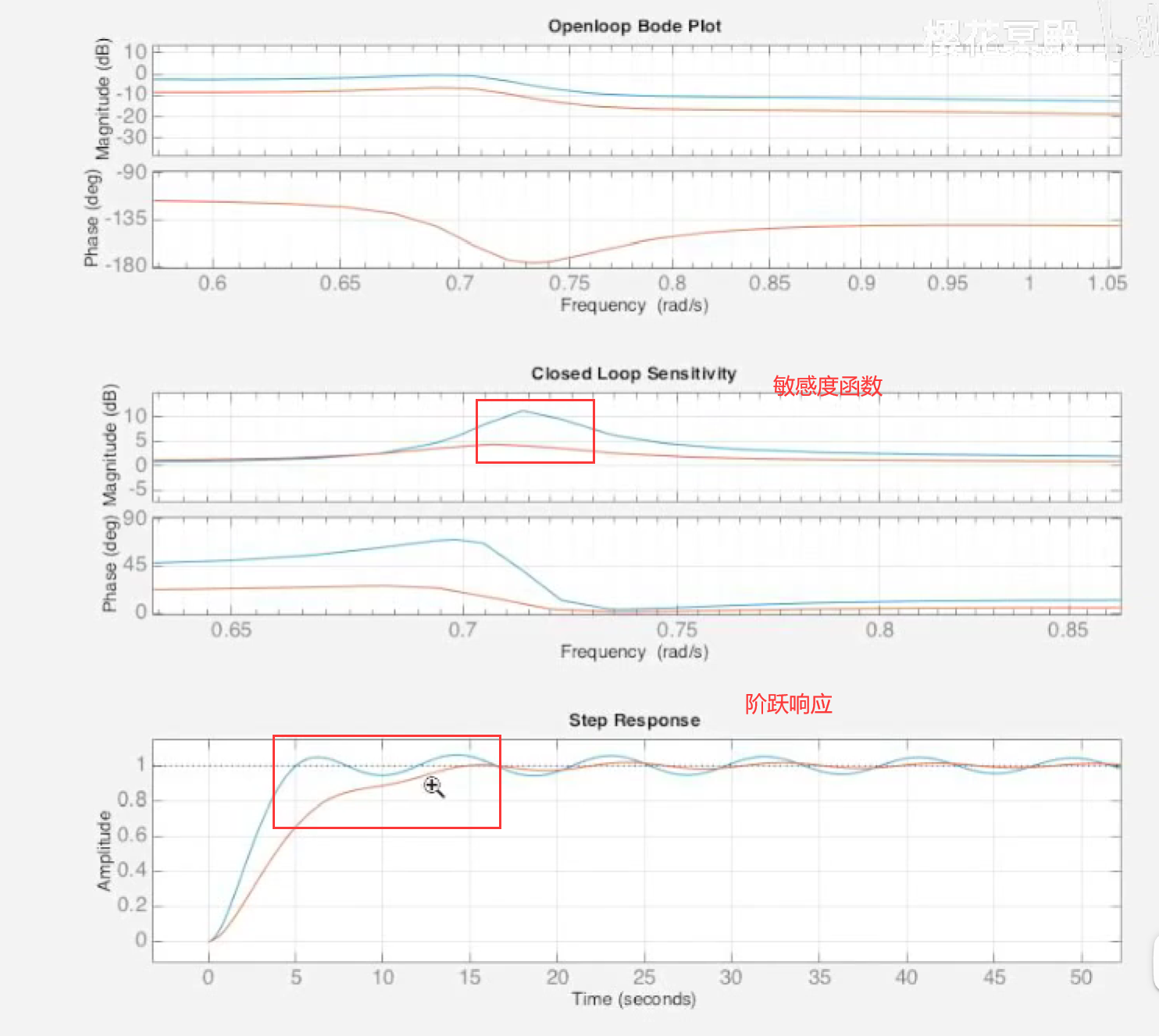
- 应用陷波滤波器. 我们观察到敏感度只在一小段频率区域内有尖峰, 所以我们可以尝试使用陷波滤波器(notch filter)来处理系统, 只使这个频率区域内的增益降低而不影响其它频率.
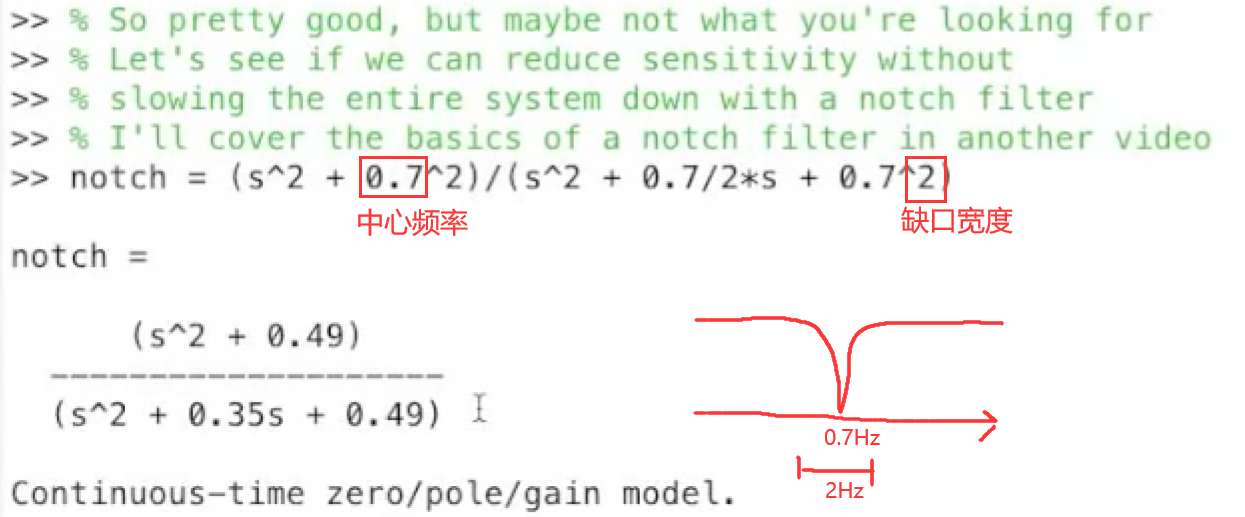
应用陷波滤波器, 也就是将滤波器与系统级联, 效果如下:
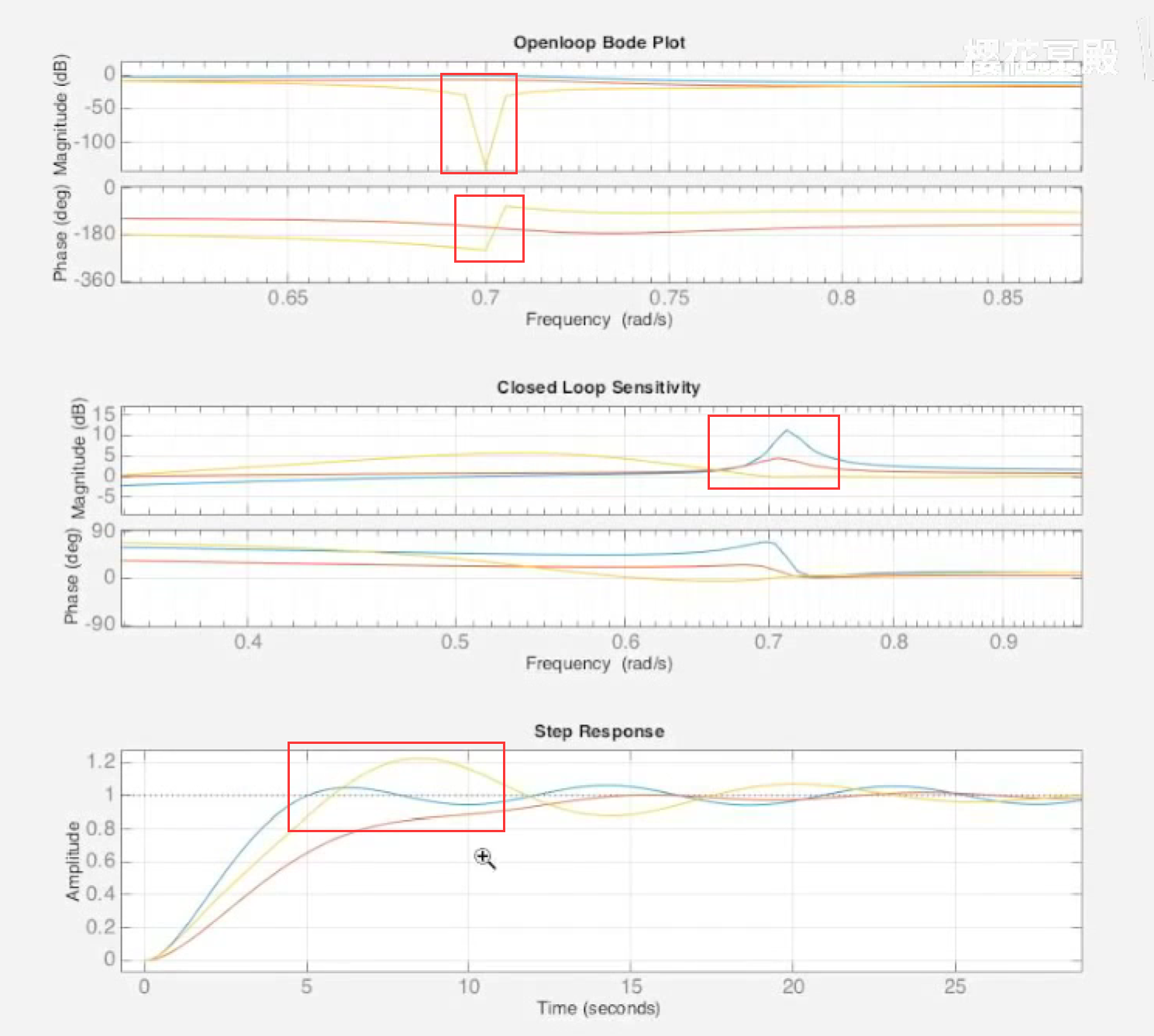
可以看到, 敏感度降低且阶跃响应没有被影响太多.